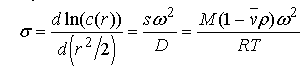Difference between revisions of "Equation 4"
Bill Bashir (talk | contribs) (Created page with "The reduced apparent molecular weight, σ, is directly available from sedimentation equilibrium: Equating equation 1 and equation 2, one obtains the fundamental equation ...") |
Bill Bashir (talk | contribs) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | The reduced apparent molecular weight, σ, is directly available from sedimentation equilibrium: Equating [[equation 1]] and [[equation 2]], one obtains the fundamental equation describing sedimentation equilibrium of a single, thermodynamically ideal protein: | + | [[Category:Sednterp]]The reduced apparent molecular weight, σ, is directly available from sedimentation equilibrium: Equating [[equation 1]] and [[equation 2]], one obtains the fundamental equation describing sedimentation equilibrium of a single, thermodynamically ideal protein: |
equation 4. | equation 4. | ||
[[File:Equation4-a.GIF]] | [[File:Equation4-a.GIF]] | ||
| − | where | + | where σ is the reduced apparent molecular weight (Ref. [[14]] [[25]]), c(r) is the weight concentration at radial position r, and the other terms are as described above or in the [[table of symbols]]. While σ may be determined from the slope of a graph of ln c as a function of (r^2)/2, sedimentation equilibrium data is analyzed best by nonlinear least squares procedures, which can accommodate more complicated cases involving association and nonideality (Ref. [[2]] [[10]] [[14]] [[26]]). |
Latest revision as of 19:10, 22 December 2011
The reduced apparent molecular weight, σ, is directly available from sedimentation equilibrium: Equating equation 1 and equation 2, one obtains the fundamental equation describing sedimentation equilibrium of a single, thermodynamically ideal protein: equation 4.
where σ is the reduced apparent molecular weight (Ref. 14 25), c(r) is the weight concentration at radial position r, and the other terms are as described above or in the table of symbols. While σ may be determined from the slope of a graph of ln c as a function of (r^2)/2, sedimentation equilibrium data is analyzed best by nonlinear least squares procedures, which can accommodate more complicated cases involving association and nonideality (Ref. 2 10 14 26).