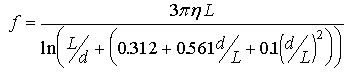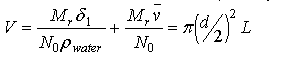Difference between revisions of "Calculating Cylindrical Asymmetry"
Bill Bashir (talk | contribs) (Created page with "The proper hydrodynamic model for molecules that exhibit an elongated shape with a uniform thickness is the cylinder. The frictional coefficient for a cylinder is: Equation 36: ...") |
(No difference)
|
Revision as of 18:54, 11 August 2011
The proper hydrodynamic model for molecules that exhibit an elongated shape with a uniform thickness is the cylinder. The frictional coefficient for a cylinder is: Equation 36:
where f is the frictional coefficient, L is the length of the cylinder, d is the diameter of the cylinder, η is the viscosity, and the constant terms are an interpolating formula for cylinders valid for values where 2 < L/d < 20. This value of f is used in equation 3:
equation 3.
and the molecular volume is computed by:
where δ1 is the degree of hydration expressed as g-water/g-protein, vbar is the partial specific volume of the protein, N0 is Avogadros number, and Mr is the molecular weight of the solute. Thus there are given two equations two equations containing the two unknowns, L and d. These two equations are solved by a Newtons roots method to estimate L and d from the experimental data. If the exact degree of hydration is not entered by the user, the degree of hydration is assumed to be zero.