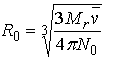As before
This section deals with calculating the equivalent radius and all directly resulting values including the minimal frictional coefficient , the maximum diffusion coefficient, and the maximum sedimentation coefficient. The starting point for hydrodynamic analysis from sedimentation data is the calculation of the expected radius for a rigid, impermeable and incompressible sphere having the identical volume as the protein of interest. This quantity is called the "equivalent radius" and is designated . As will be explained below, there is some ambiguity as to exactly how should be determined.
There have been several methods proposed for the calculation of shape or hydration data based on the hydrodynamic data available wholly (Ref. 27 29) or in part (Ref. 28 29 30 31 32) from the analytical ultracentrifuge. The Sednterp program assumes that only sedimentation data are available, and methods that rely on knowledge of the viscosity increment (Ref. 31) or the radius of gyration (Ref. 32) will not be discussed here. While this places severe limitations on the interpretation, it is reasonable for situations where either material or instrumentation is limited. Should sufficient material and equipment be available for supplementary measurements (radius of gyration or viscosity increment), then it would be wiser to conduct the additional experiments needed to complete the hydrodynamic interpretation. (Ref. 28 31 32)
In order to account for the fact that the protein is displacing solvent rather than occupying a vacuum, the value of often is calculated as in equation 21.
Equation 21:
However, there is no theoretical justification for the use of in this calculation (Ref. 9) except that reflects, in large part, the volume of solvent displaced by the protein. It is often found that calculated using equation 21 is too small, thus leading to overestimates in of the axial ratios. (Ref. 30 33) This is not surprising since includes solute-solvent interactions other than solvent displacement. Significant errors can be introduced if, for example, there is considerable electrostriction of the solvent by a highly charged protein (Ref. 6 34). Moreover, this calculation underestimates the contribution surface roughness (rugosity) makes to the protein hydrodynamics (Ref. 30).
Since there is no theoretical justification for equation 20, it has been suggested that this calculation can be made using an empirical relationship based on X-ray crystallographic structures (Ref. 28 33). Teller has described two such apparent radii (Ref. 33). The first , is evaluated as shown in equation 22.
Equation 22:
is determined from the packing volume in protein-protein complexes. A second estimate of an effective radius, , accounts for the surface roughness of the protein. For monomeric proteins, and use of in hydrodynamic calculations leads to absurdly low estimates of the hydration and axial ratio (unpublished data). Other authors have used as an estimate of the anhydrous radius, but have neglected Rs, apparently for similar reasons (Ref. 28). Use of these relationships typically yield larger values than and, consequently, smaller estimates of the axial ratios.
Regardless of whether equation 21 or 22 is used, and are considered to be the minimum radii possible for the anhydrous protein (Ref. 28 29 30 31 32 33). All evidence to date suggest that provides better estimates of the anhydrous radius. The predicted minimum frictional coefficient, (normally called ) is calculated from the Stokes-Einstein relationship using either R0 or Rp in equation 22 (Ref. 18):
Equation 23:
where η is the standard viscosity of pure water at 20 C. For notational purposes, Sednterp labels the minimum frictional coefficient fp when it is computed from Rp. Sednterp carries these calculations for both the vbar method and the Teller empirical method to their conclusion by calculating a maximum sedimentation coefficient and a maximum diffusion coefficient from f0 and fp.