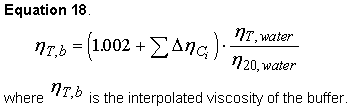Calculating Viscosity
Viscosity is a measure of the energy dissipated in a fluid in order to maintain flow. In sedimentation, the flow of interest is the movement of the protein through the solvent. For a fixed amount of energy, the greater the solvent's viscosity, the slower the protein will move. Therefore, solvent viscosity will affect both sedimentation velocity and the time needed to reach equilibrium. (Ref. 2 14 17) Excellent reviews are available describing methods for determining viscosity and for interpreting viscosity data. (Ref. 47 48) The viscosity is dependent on both the temperature and the solution composition.
Sednterp can interpolate the viscosity of a buffer from viscosity table data in the phyconst database. It must be realized that the viscosity of a sample may be affected by low concentrations of macromolecular solutes. Thus, the estimate from equation 18 is valid only at zero protein concentration. Viscosity must be measured for solutions of highly asymmetric molecules or solutions containing moderate to high concentrations of any macromolecular solute. First, viscosity increments (Ref. 8) for each buffer component are calculated by subtracting the viscosity of pure water from an interpolated single component solution at the standard temperature of 20 C.
Equation 16
where is the density increment of the ith component at concentration C, a-e are the coefficients of the least squares fit of the original viscosity data, and the factor 1.002 is used because the original fits were made from data based on the relative viscosity of water = 1.00.
Second, the viscosity of the buffer is computed by adding up the viscosity increments and multiplying by a temperature correction factor that is calculated assuming that water makes up the bulk of the temperature dependence of the viscosity. Equation 17 is the set of equations for calculating the viscosity of water at temperatures from Physical Methods of Chemistry (Ref. 49).
Equation 17