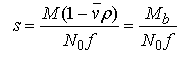Equations for s

The apparent sedimentation coefficient is determined directly from the data: Rearrangement of equation 2 reveals that the sedimentation coefficient can be determined from the slope of a graph of ln(r) versus ω^2*t, where r is the distance from the center of rotation to the midpoint of the concentration boundary and t is time. (note: More appropriately, the second moment of the boundary should be used, but for a single component the difference in s is negligible. (Ref. 2)) The interpretation of s begins by observing that:

equation 3.

where M is the solute's anhydrous molecular weight (g/mole), vbar is its partial specific volume (ml/g), ρ is the solvent density (g/ml), N0 is Avogadro's number, Mb is the buoyant molecular weight and f is the translational frictional coefficient.

For a hydrodynamically ideal molecule, all information concerning the shape and size of the molecule is expressed through f. Changes in f are propagated inversely to s. Equation 3 shows that knowledge of M and s are sufficient to determine f, even in the absence of determining D. This latter approach to the determination of f is often preferred because accurate values of M and s are generally easily obtained, but accurate determinations of D can be difficult.

For solutions containing two or more non-interacting proteins, and in cases where the boundaries are well resolved, the analyses described below may be applied to each component's boundary. It must be kept in mind, however, that the effects of solute-solute interaction are not always innocuous and they can produce measurable alterations in the shape and position of the boundaries. (Ref. 20) For cases where there is considerable heterogeneity in a sample, it is useful to examine the integral sedimentation coefficient distribution function, G(s*) or its derivative g(s*) = s*dG(s*)/ds* (ref. 60).